Combine Python Graphical User Interface with SQL Injection

Python is great language for penetration testing, I saw that people mostly develop python applications with command line versions only. How ever python have such a beautiful library named Tkinter to develop a graphical user based application, in this article we will combine Tkinter with sql injection to create a small GUI application that can check a website for SQL Injection vulnerability. In this tutorial we are going to use SQL Injection code from tutorial present at:

Use Python to automate SQL Injection!

Note: Article mentioned above is a must read, without reading the article above it might be hard for you to understand few things, but I’ve tried to explain everything in details.

This article provide you with basic understanding of how you can use python to automate SQL Injection. Now that you have good knowledge of how you can use python for penetration testing purposes we should first learn some basics about the Tkinter module.

Step 1: Install Tkinter!

Please note that to use Tkinter you should have a linux operating systems with graphics support. I am going to do this on Ubuntu Desktop 16.04 LTS.

sudo apt-get install python-tk

You can use this command to install tkinter, I assume that you already have python installed. I would recommend you to use Pycharm for basic python development.

Step 2: Create First Window using Tkinter!

If your Step 1 was successful you are ready to create your first GUI window in python. Let see how we can do that:

from Tkinter import *

root = Tk()

root.wm_title("First GUI Window")

root.mainloop()

1.  First line just imports the Tkinter module.
2. Second Line creates the Tkinter window, this will be the base window that will contain all our future widgets, buttons and text entry boxes.
3. Setting the window title.
4. This forth line of the above code is very important, if you don’t call this function nothing will happen. Tkinter actually puts all its function in an event queue, as soon as “mainloop” function is called all the functions inside the event queue gets executed and you finally get the desired GUI application.

This will be the output after you run this small application:

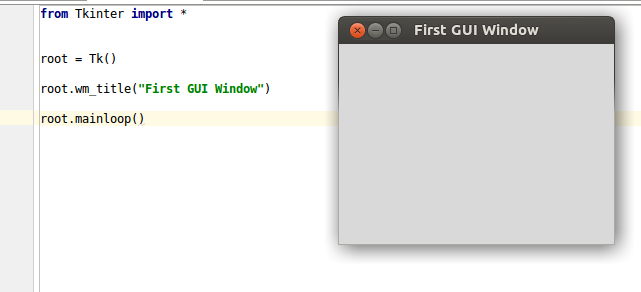
As you can see  that currently our window does not have anything inside, because we have not yet added anything. Its time we should do that now.

Step 3: Add Label and Text Box!

We will now extend our code written above and add Label and text box to our window. Following piece of code will do the trick:

enterURL = Label(root, text="Enter URL To test",fg="red")

enterURL.grid(row=0,column=0)

1. First Line creates a simple Label with text “Enter URL To test”
2. Each widget in Tkinter have a function named “grid”. This function is used to set the placement of widget on the root window, for this Label widget we set it to row = 0 and column = 0, you will see that it will be placed on first row of the window.

Your output must be similar to:

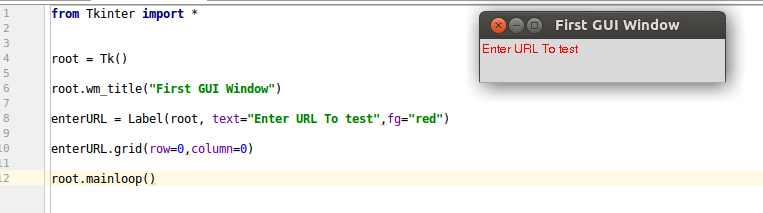
Labels are nothing but the helpful reminders to the user of our application, so that they know what to do with your application, next we will add a text box, so you will get an idea what we meant by that.

enterText = Entry(root)
enterText.grid(row=1,column=0,pady=10, padx=5)

In Tkinter text boxes are called Entry.

1. On the first line of code we’ve just created a text box using Entry class.
2. Second line places this entry box on the second row of our root window, please note that index starts from 0, so row 1 will actually be row 2 on your window.

Your current output should be something like this:

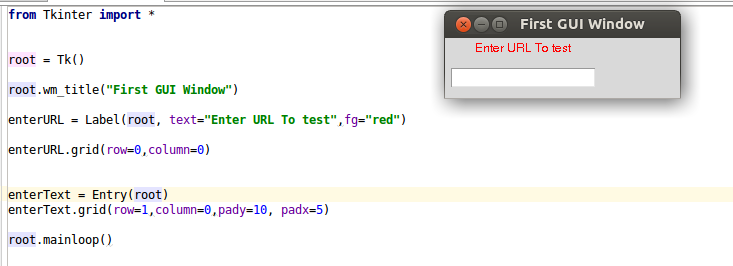
Following the same procedure mentioned above, I will add one more label and Entry box, that Entry box will get the “post” parameter that you need to check the vulnerability against. I will discuss it more later in this article. After adding another text box and label it looks like :

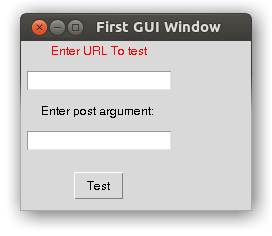
Step 4: Create Button and attach event!

As the title says we’ve to combine python graphical user interface with sql inection. To be able to do that we need to give user an option to click some button and than they get to know if website is vulnerable to sql inection or not. To do that we need to add button to our application window and than attach some event to that button.

checkIfVunlerable = Button(root,text="Test", command=testVulnerability)

checkIfVunlerable.grid(row=4,column=0,pady=10, padx=5)

1.  First line creates the button, and puts text inside the button. Last argument to this Button class constructor is “command=testVulnerability“, this argument is actually the event handler.
   • testVulnerability is actually the function that will be called when this button is pressed.
   • Before using this you have to actually define this function, than only you can create the button. For now we will create a dummy function and populate it later, you can use the code below

   • def testVulnerability():
         return 0

2. Second line of code just put this button on the 5th row of the window.

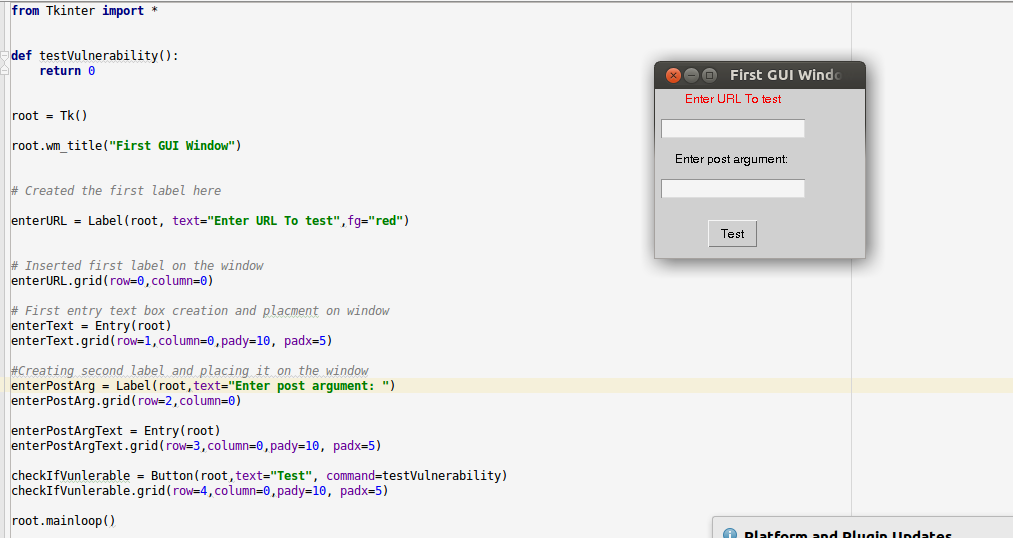
Final code up till now will look something like:

from Tkinter import *


def testVulnerability():
    return 0


root = Tk()

root.wm_title("First GUI Window")


# Created the first label here

enterURL = Label(root, text="Enter URL To test",fg="red")


# Inserted first label on the window
enterURL.grid(row=0,column=0)

# First entry text box creation and placment on window
enterText = Entry(root)
enterText.grid(row=1,column=0,pady=10, padx=5)

#Creating second label and placing it on the window
enterPostArg = Label(root,text="Enter post argument: ")
enterPostArg.grid(row=2,column=0)

# Creating post argugment entry box and placing it on the window/grid

enterPostArgText = Entry(root)
enterPostArgText.grid(row=3,column=0,pady=10, padx=5)

checkIfVunlerable = Button(root,text="Test", command=testVulnerability)
checkIfVunlerable.grid(row=4,column=0,pady=10, padx=5)

root.mainloop()

And output should be :

Step 5: Start Defining event Call Back Function

Function named “testVulnerability” will be actually called when the button is pressed. We will have to perform few things once this button is pressed and we will do them all in this function.

Get the URL and Post Argument Value

We need to get the url and post argument entered in the text box and save it in a variable so that we can later pass it to the function, that can be achieved through the Entry class “get” function. All you have to do is call this function on the Entry class object and you will get the value as string.

urlEntered = enterText.get()
postArgEntered = enterPostArgText.get()

This will save the entered url in the text box to variable “urlEntered” and post argument to the variable “postArgEntered” once the user click the button. We will pass this variable to another function, that is eventually going to test if the entered URL is vulnerable to sql injection. Our “testVulnerability” function will have the following code:

def testVulnerability():

    urlEntered = enterText.get()
    postArgEntered = enterPostArgText.get()

    value = checkIfVulnerable(urlEntered, postArgEntered)

    if value == 1:
        enterText.delete(0, END)
        enterText.insert(0,"Vulnerable")
    else:
        enterText.delete(0, END)
        enterText.insert(0, "Not vulnerable")

In this code we’ve called a function named “checkIfVulnerable“, this function will be our key function and it is yet to be defined. We will define this function in our next step, but if this function respond with value “1” we will know that the entered URL is vulnerable and if responce is “0” than entered url is not vulnerable.

This function takes 2 arguments, first is the “urlEntered” and second is the “postArgEntered“, we have just saved those values in the variable above and now they are passed to the function.

Step 6: Create a simple PHP Script!

Before writing our “checkIfVulnerable” function, we will write a simple PHP script that will be vulnerable to sql injection.

<?php


// Creating a database connection, because sql injection starts with a database :) , Please note this database must exist on your server.

$serverName = "localhost";
$userName = "admin_test";
$password = "cyberpersons";
$databaseName = "admin_test";


// this argument will be passed from our python script

$userFromArg = $_POST['userid'];

$dbcn = new mysqli($serverName, $userName, $password,$databaseName);

if($dbcn->connect_error)
{
    die("Connection failed:". $dbcn->connect_error);
}



$sql = "SELECT userID, userName AS max FROM user where userID=$userFromArg";
    $result = $dbcn->query($sql);

    if ($result->num_rows > 0) {
        $row = $result->fetch_assoc();
        $name = $row["userName"];
    echo $name;
    }else {
        echo $fail;
        exit();
    }
  
  
?>

This is a very simple PHP script, all it do is takes a post argument named “userid”, than it runs an SQL query against this user id and print the name of this user id, we will try to penetrate this argument. 🙂

This script is also hosted at : http://check.cyberpersons.com/ProjectDev/vulnTest.php

If you pass the userid = 1 , your HTTP response will be “Usman Nasir”, now on userid argument we will inject our adapting payload that is also explained and used here. I must say that you must read about the adapting payload before continuing. What adapting payload do is add an extra 1 second in your normal response time only if your application is vulnerable to sql injection.

For example if your normal response time was 0.5 seconds, with adapting payload it will be around 1.5 seconds and that is how you know that you need to secure your code.

Step 7: Define “checkIfVulnerable” function!

I think this function will be the most fun part of this article. Also we have pieced together everything to be fed to this function, so lets start this  function.

def checkIfVulnerable(url,postArg):

    # build the key value pair post argument to be send to the url

    data = {'userid': postArg}

    # lets prepare the post request

    result = requests.post(url,data)

    # now calculate if the responce time is greater than 1 second most probably application is vulnerable to sql injection

    if float(result.elapsed.total_seconds()) > 1:
        return 1
    else:
        return 0

This will be the final shape of our “checkIfVulnerable” function. I’ve made a use of another module named “request”, which is explained here. If you don’t want to read the other article I will explain about the request module a little here. All it do is simulates your browser, it sends a HTTP web request to your desired URL and create a response object, and the response object have all the properties of normal HTTP response. Lets get back to our fun function.

1. First this function prepares a key-value pair of arguments to be sent along the post request and the key value is saved in “data” variable.
2. We than sent a post request to a url entered in the text box.
3. Finally it checks if response time was greater than 1, it returns 1 as its return value to the calling function and 0 otherwise.

You might remember when we was defining our event call back function in Step 5, we said that we will use the value returned from this function and we just did. If this function returns 1, our event call back function will populate first text box with “Vulnerable” and “Not Vulnerable” otherwise. Fill in the form below to download complete source code of the completed application:

[email-download-link namefield=”YES” id=”3″]

Step 8: Simulate the application

We will now run and simulate this application, on your first run you will see the first window, please fill in as filled in the image below.

 

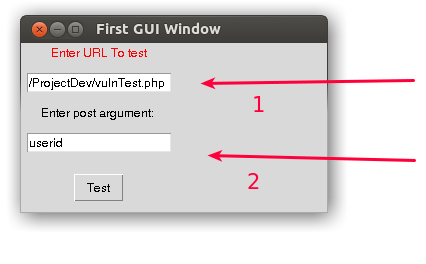
1. Enter complete url where your web application is located (I used : http://check.cyberpersons.com/ProjectDev/vulnTest.php ).
2. The post argument you need to test against.
3. And than click Test.

If your application is vulnerable, you will have output something like:

Final Words

This is one of the very basic application that you can build, you can customize it to test against multiple post arguments at once, or multiple URLs. You can also define your own payloads to be sent along with the post request. If you have more than 100 payloads you can save them in the list and iterate through them, and record the response of each request.

Feel free to ask any questions in the comment box below.